
Replay: Modern cameras have incredible dynamic range - but you can only access it if you use a "log" or "Cine-style" mode when you record. Phil Rhodes explains how this works, and wonders why there are so many non-standard ways to do it!
In some ways, life would be a lot more convenient if our eyes were more predictable in the way they respond to light. If we had linear eyes, manufacturers would have a much easier time building cameras and post gear that might be as transparent to our eyes as current audio technology is to our ears (although they're not linear either). Since we don't have linear eyes, however, it's difficult not to see common approaches of recording luminance as the equivalent of the crackly old 78RPM gramophone records of the early twentieth century.
Perhaps I'm being too harsh. We have recently seen a renaissance of sorts in the form of logarithmic, or pseudo-logarithmic, luminance encoding. This can sometimes give camera people access to something that isn't that dissimilar to what was available from film. The problem is that every camera manufacturer in the world is coming up with their own specific solutions, creating incompatibility and requiring a degree of on-set picture engineering that was never required in the photochemical discipline.
We've talked about log before, and we'll talk about it again, but let's briefly recap before we dive into the meat of the problem.
Log versus Linear, Explained
The human eye responds to light more or less linearly as the real light intensity doubles. This is familiar to photographers as an exposure value, where increasing an exposure value by one always looks like the same amount of additional brightness, even though every increase in visible brightness actually represents a doubling of light intensity. If we view a scene with a single 100W light aiming at it, we could call light 100. Let's assume the scene is comfortably exposed in these circumstances, so we can call it brightness 1. To double the amount of light, we might add another 100W light, so light is 200 and brightness is 2, which is fairly intuitive. But to increase the apparent brightness by the same amount again, so that brightness is 3, we need to double the amount of light again, so that light is 400. This is of course not new; when the system of f stops and exposure value was developed, we knew that linear apparent brightness increase requires successive doubling of the amount of light.

[Fig. 1: Doubling light increases brightness linearly.]
Recording log is a way of using this to improve recordings. Assume that the image data from a camera's sensor is linear; every time we double the amount of light, we double the digital numbers. That isn't how many sensors really behave, but it's a useful approximation for now. We can store this data unmodified, but every unit of apparent increase in brightness then requires a doubling of the stored digital value, so bright highlights end up occupying a huge range of values. Assuming that we expose a subject such that its value in an 8-bit image is 8, if we then open up one stop, its value will be 16. If we open up another stop, its value will be 32. Another stop, 64, and so on, to 128 and 256. Since there are 128 values between 128 and 256, we're using 128 values – that is, half of all the values we have available - to store the single brightest stop of luminance information. But since there are only 8 values between 0 and 8, we're only using 8 values to store the dimmest stop. The following drawing shows an approximation of the greyscale being recorded by each range of digital code values, with red marks indicating exposure values (or a series of f-stops, if you like).
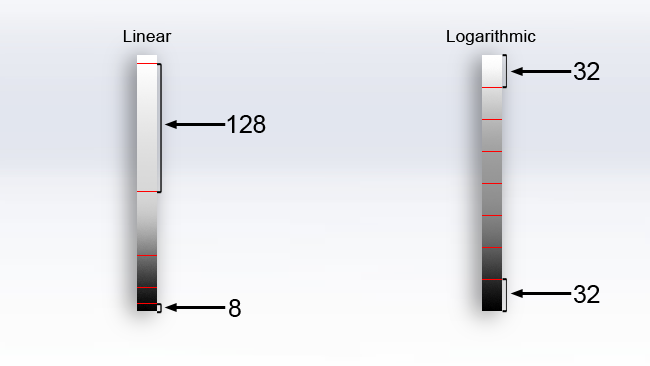
[Fig. 2: Linear and logarithmic code value distribution]
The "linear" chart shows the successive doubling of actual exposure doubling the recorded value (we'll discuss the "Logarithmic" chart on Page Two). Notice that the large 128-value range at the top of the linear chart doesn't actually look like a large change in brightness, because of our nonlinear eyes, but we end up using 128 values to represent it anyway because it represents a large increase in light level.
One solution to this imbalance is simply higher overall precision. Even early digital ENG cameras used 16 or more bits when processing their sensor data. More than 65,000 values are then available, and many stops of dynamic range can be stored with workable precision. While the march of technology is making storage easier, though, we'd rather avoid storing 16 bit data, and happily, we can, without any meaningful loss of quality. Converting the data such that each f-stop occupies the same range of values is straightforward, a base-2 logarithm, such that doubling the light falling on of an object exposed at (say) value 32 moves it to value 64, and doubling it again moves it to value 96. In this graph, we can see the output of a notional linear 8-bit camera (let's say there are 12 stops of dynamic range between "black" and "white"), shown in red, and the effect logarithmic processing has on the data, shown in blue:
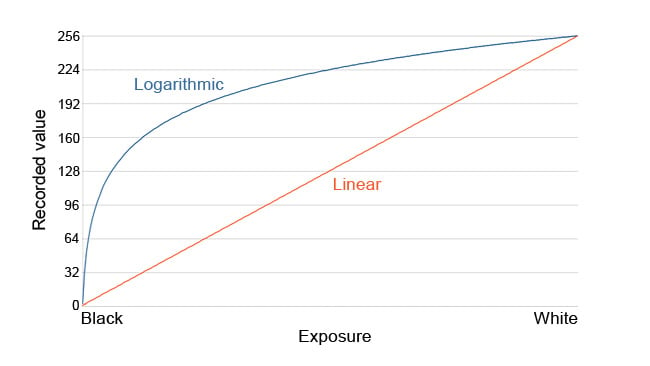
[Fig. 3: Linear light vs log2]
As we can see, the processed version rushes quickly up through the shadow detail, ensuring dimmer picture information is represented with a reasonable number of code values, then flattens in the highlights, reducing the number of values used to represent them. The same number of values are used per stop. It's also intuitive to see here why log images look so low in contrast: blacks are massively lifted. Referring back to fig. 2, notice that the "logarithmic" chart includes roughly the same amount of visual difference in brightness in every 32-value, one-stop range.
The Trouble with Log
The key problem is that few cameras actually work this way. Sensors are not ideal and everyone wants pictures which look subjectively nice, which is a matter of opinion, subject, and photographic intent. Real world log profiles usually give us an approximation of log, modified by the manufacturer to achieve some goal. Generally, each f-stop's worth of information occupies roughly the same range, but this can break down at the extremes of light and dark, and variations may be offered with the intention of supporting a particular photographic intent, in the same way as a Canon DSLR's picture styles.
When the output from such a camera is displayed, we must know how the picture has been treated so that we can undo that treatment and display it correctly. Because of all this variability, monitoring equipment must have specific knowledge of the camera's luminance handling behaviour. Using the wrong anti-log curve can produce images with crushed or floating blacks, noise, clipped or dulled highlights, or almost any other imaginable problem, causing a cinematographer to make misguided decisions about lighting and exposure. With cameras generally capable of using different curves at the touch of a button, and with post-production software offering even more flexibility, it's easy for serious problems to arise.
The underlying issue is a lack of standardisation. Taking calibration into account, any viewing situation currently needs to take into account three or four different things (the camera's log curve, any creative curve, any calibration, and then the monitor's anti-log curve), and that's true on set and throughout post, representing a risk of, at best, inaccuracy, and, at worst, critical picture quality issues. Nobody's proposing a return to the days of ITU Recommendation BT.709 – a standard closer to linear than log – but normalisation is long overdue. The counterargument is that all cameras are different and attempts to force them into a single specification would risk compromise, but the existence of previous standards – such as 709, and the picture styles available on Canon DSLRs with their selection of sRGB or Adobe RGB output – suggests that it's workable for manufacturers to offer distinctive and useful options within a standardised framework.
I'm ready to be convinced that every camera system needs its own custom setup, and I stand ready to retract all of this in that case. Until that point, I shall hope that in a few years we'll be looking back on the current situation and chuckling at how poorly organised everything used to be.
Tags: Technology Production


Comments