Why fast lenses are difficult to make

Replay: Phil Rhodes is your guide to an exploration into lens optics that helps explain why fast zoom lenses are both huge and expensive.

Speed obsession in lenses has its roots in the 1960s, but persists even to this day of 800-speed cameras. There's probably a sorry tale about impatience and shrinking lighting budgets in there somewhere, but the upshot is that Canon's recent 18-80mm lens, aimed squarely at the market of big-chip documentarians with low-cost cameras, has been criticised for its t/4.4 performance.

Engineered for speed

Curmudgeonly as such criticisms may seem, there's some fundamental engineering going on which is worth understanding. It helps us choose glass, put it to the best possible use and understand why that oh-so-desirable lens set costs as much as a house and, furthermore, requires us to hire a large person simply to carry it around.

The actual image that makes it through most practical photography lenses to hit the sensor is, subjectively, pretty dim. A miniature person standing inside the lens cavity, with dark-adapted eyes, would probably be able to see an image exposed for sensitivity of a few hundred ISO. They'd also be able to provoke endless consternation by making rabbit shadows on the sensor. Overall, though, modern sensors and photochemical film are required to resolve an image out of something that really isn't a lot of light. Most of us understand that smaller f numbers mean more light and larger ones mean less, but even that's hardly instinctive.

What's going on here is maybe best understood in terms of a simple single lens, projecting an image onto a screen. Let's assume there's a single point of light, like a very distant candle flame or a notional point on the surface of an object that's reflecting light. Light radiates from this point in all directions and only that which happens to hit the lens might make it onto the sensor to form part of the image.

The lens captures any light which reflects into it from the subject.

If we use a bigger lens of the same focal length, we get the same view, but more of the light will be intercepted and focussed to form a brighter spot on the sensor:

A larger lens captures more light, forming a brighter image of the same size.

Anyone who's seen a set of prime lenses will be aware that the longer focal lengths get larger to achieve the same F-stop and that lenses which are both fast and long get very big very quickly. The reason for this is pretty easy to understand: the longer focal length lens produces a smaller field of view by enlarging the image and, if we blow up a picture of something, we're spreading the same amount of light out over a larger area:

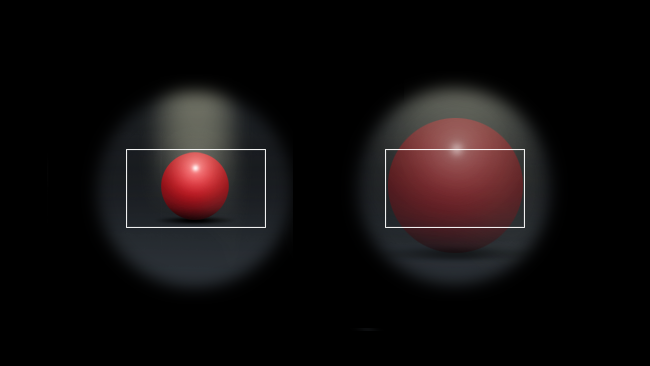Longer focal lengths spread the same amount of light over a larger area, reducing the brightness of the image.

So far, so obvious. But what happens when we choose lenses with very short focal lengths, which also tend to be expensive, bulky and slow, just like long lenses? The magnification is minimal, because we're showing a wider field of view, making subjects smaller in relation to the size of the frame, so it should be relatively easy. The difference is that this isn't directly to do with aperture: it's due to the geometry of getting that wide angle image to land properly on the sensor. This is especially problematic in situations where you can't put a lens element, say, 18mm from the sensor in an 18mm lens because that space is occupied by other parts of the camera. Solutions to this are too involved to go into here, but suffice to say that they affect both physical bulk and f-stop.

Stop discussion

So, we require a lens of a larger diameter to achieve a given stop at longer focal lengths. Stops are therefore ratios and have been described as such since at least 1874, when John Henry Dallmeyer referred to calculating "intensity ratio" of a lens by dividing "the focus by the aperture." The actual calculation is the ratio between the focal length and the size of the hole through the middle, which is why we describe them using the f/ notation. A lens of f/2 aperture implies the hole down the middle is half the focal length; 50/2 is 25mm. This is why lower numbers mean brighter images and why long lenses, such as the Canon 20x50 (implying a maximum focal length of 1000mm) are both physically enormous and still not all that fast. To achieve f/2 at the long end of the zoom, such a lens would need to be at the very least 500mm across (that's nearly twenty inches, Americans).

To be complete, the term for the effective hole through the middle of a lens is the 'entrance pupil' and, no, that unfortunately doesn't mean it's as easy as measuring the diameter of the front of the lens. In theory, the entrance pupil is the size of the hole through the lens as viewed through the front elements of that lens. Those front elements may magnify or reduce the apparent size of the aperture, so it isn't that easy to measure. A technique for doing it was described, by Dallmeyer, involving projecting light backwards through the lens to cast a shadow of the aperture on a screen placed in front of it.

Perhaps the last question to answer is why f-numbers are such an odd sequence. The next stop above f/1 is 1.4, followed by 2, 2.8, 4 and 5.6. Contrary to popular belief, there's nothing special about f/1 and it's possible for a lens down to f/0.5 to be made with conventional techniques or even lower, if there isn't an air gap between the back of the lens and the sensor. The reason they're an odd sequence is to ensure reciprocity – that is, to ensure that doubling film (or sensor) speed has the same effect on exposure as reducing aperture one stop. The aperture is roughly circular, so what we care about is the area of a circle, but the stops themselves refer to the diameter of the circle. Calculate the area of the circle, according to πr2, and it becomes clear that the area doubles with each stop. Assuming f/2.8 has an aperture of diameter 10mm, the area is 79mm². Increase to f/2, so that the aperture has a diameter of 14mm, and the area is 154mm², or about twice as much. Increase to f/1.4, with diameter 20mm, and the area becomes 314mm², and so on. There's some small inaccuracy because f/1.4 is rounded down from 1.4142 (the square root of two), but the intent is clear.

Many medium-focal-length lenses, such as this 50mm 1.8, are both fast and affordable.
Notice the large entrance pupil.

All of this is why fast lenses are big. Take heart, though: the simpler optical layouts of prime lenses make life a lot easier. You can get a 50mm Nikon E-series prime on eBay for under £100, which opens up all the way to f/1.8. Fifty divided by 1.8 only requires the entrance pupil to be a shade under 28mm in diameter, which is easily doable.

Just hire a good focus puller.