There's a lot more to bitrates than you think

When is the bitrate not the bitrate? Codecs are a compromise between quality and storage space used. Phil Rhodes explains why the bitrate on the spec sheet is not always what you'll get when you record for real.

Most people have a fairly instinctive understanding of higher bitrates meaning better pictures. Cameras and recorders are often promoted with references to the bitrates they can record and distributors may require certain minimum bitrates for different types of production. There are arguments over how representative of image quality a single number can be, given the fact that different encoders achieve different results at the same bitrate. What's perhaps a bit more off-putting, though, is that if we start looking at camera files with analytical tools, we discover that very few video encoders actually achieve the bitrates that are mentioned in promotional material.

That occasionally makes people ask awkward questions, but it really isn't the result of some giant swindle. Compressing pictures isn't an exact science and when we're preparing video for recording on a flash card or streaming over a network, it's crucial that we don't end up with more than the card or network link can handle. Create too high a bandwidth and we end up dropping frames, which is disastrous; we must not go over the limit. We can go under the limit, at the cost of image quality, but we must not exceed it.

This test image was compressed with a common camera codec using the combinations-of-sine-waves technique described in the article

At 1000%, viewing the area boxed in red above, we can see the edges of the eight-by-eight pixel blocks used to perform the compression

The question, then, is why it's not generally possible to ensure that (for instance) a ProRes 422 file always achieves exactly 117Mbps as Apple's own format specifications suggest it should?

This is easier to understand in the context of how (most) compression techniques work. An eight-by-eight block of pixels can be thought of as 64 brightness values. Put those brightness values in a chart or graph and they draw an irregular wobbly line. One of the most common techniques is to describe that wobbly line as combinations of sine waves or other mathematical shapes. The wobbly line can be approximated by adding together various sine waves in various proportions. If we ignore (or store with reduced precision) the smaller, higher-frequency wave shapes that make up our wobbly line, we still end up with roughly the same wobbly line, but we can store it in less space.

The graph of pixel brightnesses (left) can be closely approximated by adding together sine waves (right)

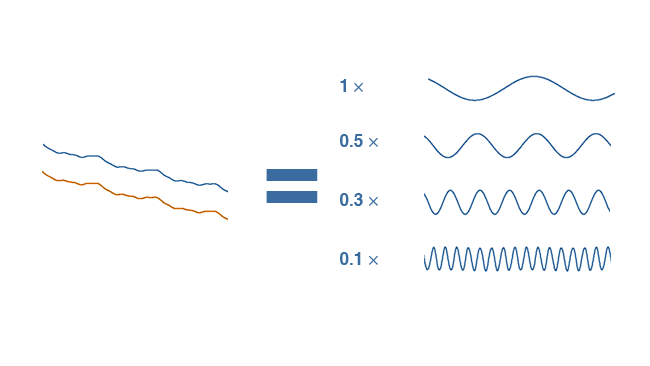
If we store the numbers with much less precision, the graph shape looks almost exactly the same. The uncompressed graph is shown in orange for comparison

This is how everything from ProRes and DNxHD to DVCAM and JPEG works. The problem is that we don't know how many of those smaller, high-frequency waves are in a particular block of pixels until we convert those pixels to a pile of waves. There might be a lot of them. It might not be possible to overlook many of them without taking all the high-frequency detail out of the image. The decision on how many of those small, less significant wave shapes we can get away with ignoring may need to be modified for different parts of the image. Simple flat areas like skies can be encoded simply. Fine detail, not so much. We can't tell how this is going to work out until a lot of the mathematical work is done, so the only way we can target a constant bitrate is to keep redoing the work with a different threshold for what we leave out.

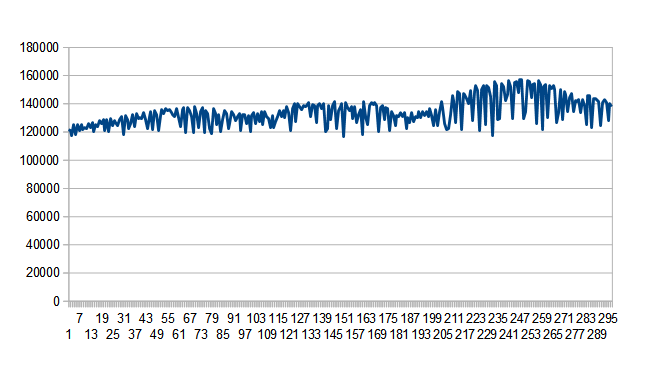
Example bitrates from a common camera codec. The bitrate requested was somewhere around the top of the graph

So, even when an encoder does target a constant bitrate, there's a limit to the fineness with which the compression settings can be tweaked. That's especially true if the encoder isn't a piece of software running on a big workstation. The hardware encoders in cameras often can't spend much, if any, time redoing work until the results hit a certain target. For situations where it's very important to maximise quality, such as on a restricted-bandwidth internet stream or Blu-ray disc, it's sometimes possible to have the encoder go over the material more than once. In this situation, it will use information on how the compression of a particular frame worked out before in order to get closer to an ideal bitrate.

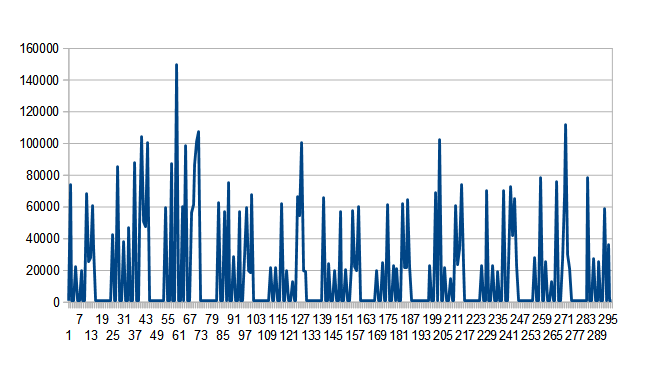
The situation becomes even more complicated with formats like H.264. This is the actual bitrate over 300 frames of an HD file. The requested rate was 20Mbps_ the actual average is about 18Mbps

But it'll never be perfect. Some frames – black pictures, for instance – are so simple that they'll always represent a dip in bandwidth, but even for complex images, it's quite normal for quoted bitrates to be a target, or even a ceiling, rather than a precise specification.

Main image - Shutterstock