

There's no getting away from it, if you want that big budget cinema look there is often no substitute for simply having a really big light source.
Quite often, someone will pull out a pocket-sized, battery-powered light, place it a foot from the subject and shoot it at ISO 3200. That makes battery-powered lights look powerful or cameras look sensitive, or some combination of the two, but it doesn't tell us much about how light behaves in a larger, more challenging situation.

Lights get dimmer the further away we are. Here's how
Because our eyes and our brains adjust to things automatically and almost invisibly, it's easy to miss just what a range of brightness exists in the real world. A typical 100W LED might achieve 30,000 lux, which sounds like a lot until we realise that we have to be within about 18 inches of it to get that reading. Sunlight, meanwhile, is coming from a source about 150 million kilometres away and frequently exceeds 110,000 lux on a bright day. Some movie lights can equal or exceed that, but only over a very small area with narrow beam settings at short ranges.
But very few people actually need to achieve the levels of light created by the sun. High framerate shooting and the need to fill sunlit shadows are pretty rare. The reality is that we don't generally need all that much light in one spot, but we do quite frequently need light to cover a reasonably large area, because, critically, this is cinema, and our photographic subjects move.
The inverse square law
It's pretty instinctive, for most people, that if we take that pocket-sized, battery-powered light and place it three feet from the subject, by the time the subject has walked, say, six feet further away, the light will have fallen off dramatically. Most people are aware that this behaviour is controlled by the inverse square law. It's easy to picture light radiating from a point in space, getting weaker as it spreads out. It turns out that the rate at which the light level reduces is equal to one divided by the square of the distance. A point light source – a bare lightbulb, for instance - which measures 1000 lux at five feet will have fallen off to 250 lux at ten feet away. Ten is twice two, two squared is four, and one over four is a quarter.
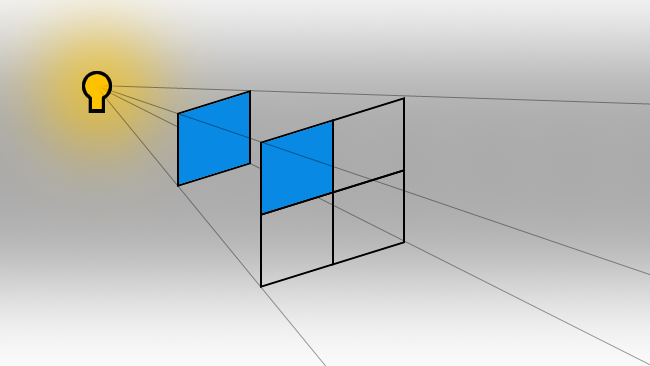
The inverse square law is easy to understand visually. Double the distance and the light decreases by three quarters. The blue squares are equal in area
In theory that only works for point light sources. Lights with reflectors and lenses, especially narrow-angle devices such as a Molebeam with its large parabolic reflector, or even a pocket flashlight, work differently. That's why companies like Arri provides their photometric calculator http://calc.arri.de/calculator which contains data about how much light their products will land on an object at various distances. Still, in situations without complex optics involved, where the size of the light source is a small fraction of the distance to the subject, the inverse square law will remain fairly accurate. This even works on things like diffusion frames, so long as they're a distance equal to several times their own dimensions away from the subject (and therefore less useful as diffusion, but that's a subject for another day.)
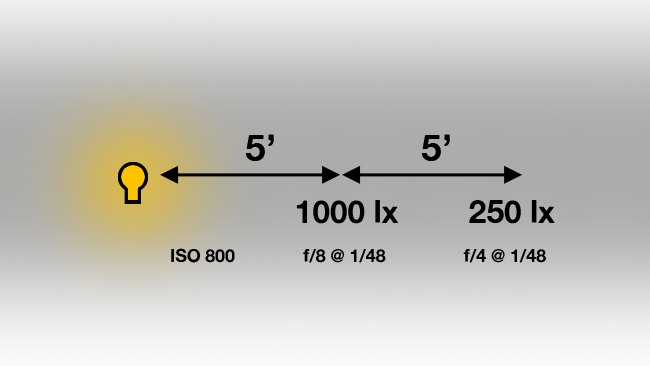
Double the distance, lose two stops. It makes sense instinctively
But why does this help us shoot moving objects? Well, let's look at a graph of the way light falls off as distance increases. The distances and light intensities given here can be in any units you like – the issue is the shape of the graph, which will hold true in all cases.
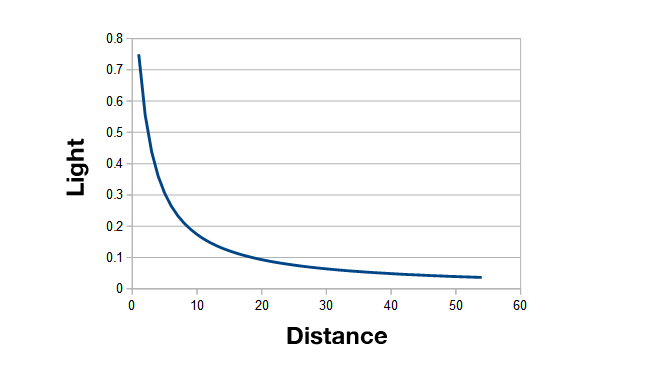
Falloff is initially steep but flattens off at longer range
At short distances, light falls off quickly, but the curve flattens out quickly. At distances between five and ten, light reduces, as we saw above, to 25%. That's a two-stop reduction in exposure. By three, we're down to 10% of the original light output, representing more than three stops of reduction.
Let's say we start further away, though. If we start at distance 40 and expose for that, by the time we've moved to distance 50, light has only dropped off a small amount. Yes, by the time we get to distance 50, there's only a small amount of the original light left, but assuming we expose for that, at least the people on screen can walk around without fading into the darkness. The losses are much less extreme with lights using lenses, which most of them do, but – here it comes – that's why we sometimes need really big lights.

Really big light
Those giant HMIs aren't up there on that cherry picker because the director of photography needs the amount of light they produce at ten feet. Even the largest lights can't compete with sunlight over large areas. That's (usually) not the point. The point is to create a setup where the light is dozens of feet away. People can walk around, where a scene can be blocked and staged without unmanageable variations in exposure. This is one of the things that most obviously separates big, expensive productions from smaller, less expensive productions – the fact that lower-budget scenes are often very static because big stuff takes big lights, far away.
18K LEDs, please.
Title image: Shutterstock - Lou Oates
Tags: Production


Comments